VBA - Beep an Octave

A piece of trivia whilst I'm prepping other meatier posts...

PC Beep can change its note

Whilst I get the Python music stack working, a little code to show that the humble console beep can in fact have its note frequency changed. The following beeps from Middle C up through the octave.

Option Explicit

'http://www.devx.com/vb2themax/Tip/18340 Francesca Balena
Private Declare Function BeepAPI Lib "kernel32" Alias "Beep" (ByVal dwFrequency _
    As Long, ByVal dwMilliseconds As Long) As Long
    
Private Const lMiddleC As Long = 257 'https://pages.mtu.edu/~suits/notefreq432.html

Sub Test()
    
    Dim lNoteLoop As Long

    Dim i As Long
    For i = 0 To 12
    
        lNoteLoop = lMiddleC * (2 ^ (i / 12))
    
        BeepAPI lNoteLoop, 500
    Next

End Sub

Are black and white keys cyclically asymmetric?

Also on music trivia, a little program that illustrates that an octave has 7 white keys and 5 black keys and that if one shifts one key at a time down the keyboard (or up, doesn't matter) that the configuration of black and white keys is unique.

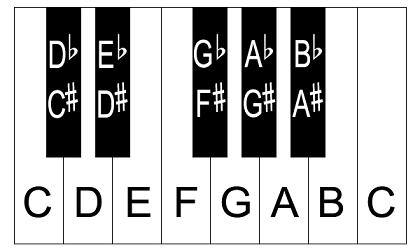
Option Explicit

Sub Test()
    '* as per diagram http://www.piano-keyboard-guide.com/wp-content/uploads/2015/05/piano-keyboard_diagram_2.jpg
    Dim sKeys As String
    sKeys = "WBWBWWBWBWBW"
    
    Dim sShiftingKeys As String
    sShiftingKeys = sKeys
    
    Debug.Assert Len(sKeys) = 12


    Dim dic As Scripting.Dictionary
    Set dic = New Scripting.Dictionary
    
    dic.Add sKeys, 0
    
    Dim lLoop As Long
    For lLoop = 1 To 11
        
        sShiftingKeys = Right(sShiftingKeys, 1) & Mid(sShiftingKeys, 1, 11)
        dic.Add sShiftingKeys, 0
    Next

    Debug.Print VBA.Join(dic.Keys, vbNewLine)

End Sub

The above code outputs the following unique set of combinations (I think the uniqueness is driven off 7 and 5 being prime numbers)...

WBWBWWBWBWBW
WWBWBWWBWBWB
BWWBWBWWBWBW
WBWWBWBWWBWB
BWBWWBWBWWBW
WBWBWWBWBWWB
BWBWBWWBWBWW
WBWBWBWWBWBW
WWBWBWBWWBWB
BWWBWBWBWWBW
WBWWBWBWBWWB
BWBWWBWBWBWW